線形代数 - Fight4354

この 2 日間の学習プロセスで線形代数の理解が徐々に明確になってきました。この投稿では、いくつかの重要な新しい内容をまとめます。

行列や特異値に直面したとき、次のような認識を持つべきです：
✅ 行列は空間の操作器です
✅ 特異値分解は行列の本質を分解します：回転 → 伸縮 → 回転
✅ 特異値の大きさの順序は、行列がどの方向に本当に力を持っているか、どの方向が無駄であるかを教えてくれます

1. 正規直交行列#

正規直交行列（Orthogonal Matrix）の核心定義

$n \times n$ の実行列 $Q$ が次の条件を満たすとき、

$Q^{\mathsf T}\,Q \;=\; Q\,Q^{\mathsf T}\;=\;I_n$

$Q$ を正規直交行列と呼びます。
ここで $Q^{\mathsf T}$ は転置、 $I_n$ は $n$ 次の単位行列です。

逆は転置です

Q^{-1}=Q^{\mathsf T}

計算が簡単で、数値的に安定しています。
正規直交行列は「内積を保持する」実行列です—— それは座標系を回転または反転させますが、決して伸縮や歪みを行いません。

2. 尖括弧#

ここで

\langle q_i,\;q_j\rangle

は「内積 (inner product)」の記号です。最も一般的な状況 —— 実数ベクトル空間 $\mathbb R^n$ —— は、私たちがよく知っている点積（dot product）と同等です：

\langle q_i,\;q_j\rangle \;=\; q_i^{\mathsf T}\,q_j \;=\; \sum_{k=1}^n (q_i)_k\,(q_j)_k.

3. 行列の位置交換#

1. 左側の $Q$ を消去します

$S$ の左側にあるのは $Q$ です
それの逆 $Q^{-1}$ を左から掛けます：

Q^{-1}\,A \;=\; \cancel{Q^{-1}Q}\,S\,Q^{\mathsf T} \quad\Longrightarrow\quad Q^{-1}A \;=\; S\,Q^{\mathsf T}

注意：

左右を一致させて左から掛ける必要があります；

$Q^{-1}$ を右側に掛けようとしないでください（それは積の順序を乱します）。

2. 右側の $Q^{\mathsf T}$ を消去します

$S$ の右側にあるのは $Q^{\mathsf T}$ です
それの逆 $(Q^{\mathsf T})^{-1}$ を右から掛けます：

Q^{-1}A(Q^{\mathsf T})^{-1} \;=\; S\cancel{Q^{\mathsf T}(Q^{\mathsf T})^{-1}} \quad\Longrightarrow\quad S = Q^{-1}A(Q^{\mathsf T})^{-1}

もし $Q$ が正規直交行列であれば、 $Q^{-1}=Q^{\mathsf T}$ となり、

S \;=\; Q^{\mathsf T}\,A\,Q.

なぜ順序を逆にできないのか？

一度でも間違った側で掛けると、記号が「挿入」されて別の位置に移動します：
$AQ^{-1} \neq Q^{-1}A$ 。
等号の両辺で必ず 対称的に 同じ操作を行わなければ、等式は成り立ちません。
これは本質的に関数の合成順序や座標変換の順序と同じです：どの変換を先に行うか、どの変換を後に行うかは、積の対応する位置に書かれ、決して自由に交換してはいけません。

4. 相似対角化行列#

相似対角化行列（一般に「対角化可能行列」と呼ばれる）は次のように定義されます：

ある可逆行列 $P$ が存在して、

$P^{-1}AP = D,$

ここで $D$ は対角行列です。
このとき $A$ は相似変換によって対角化できる、または略して $A$ は対角化可能であると言います。

対角化の「機械的プロセス」

固有値を求める： $\det(A-\lambda I)=0$ を解きます。
固有ベクトルを求める：各 $\lambda$ に対して、 $(A-\lambda I)x=0$ を解きます。
$P$ を組み立てる： $n$ 個の互いに無関係な固有ベクトルを列として行列 $P$ に配置します。
$D$ を得る：対応する固有値を対角線に埋め込みます： $D=\operatorname{diag}(\lambda_1,\dots,\lambda_n)$ 。
これにより $A = P D P^{-1}$ となります。

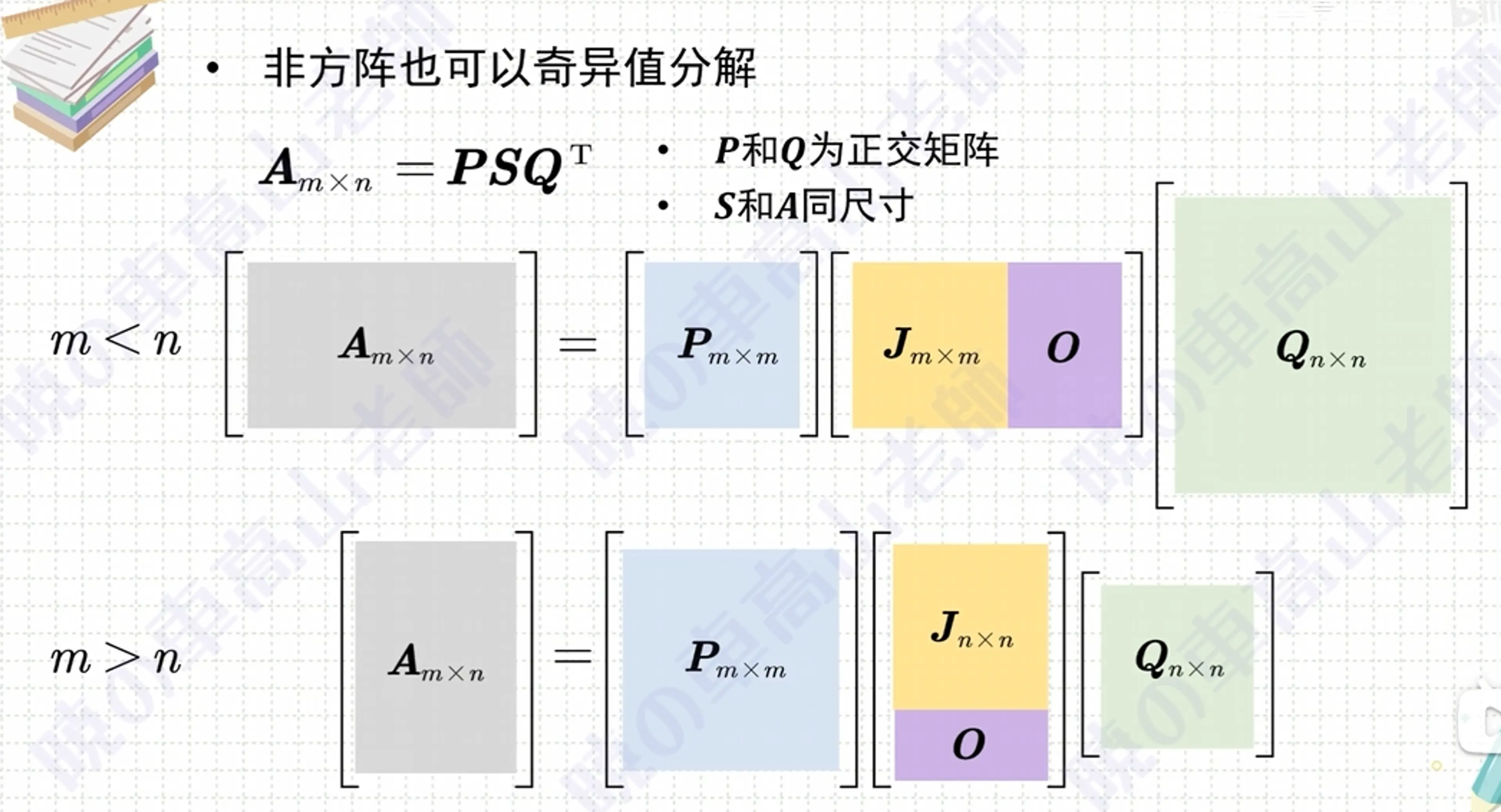
5. 特異値分解#

A \;=\; Q\,S\,Q^{\mathsf T} \quad\Longleftrightarrow\quad S \;=\; Q^{\mathsf T} A Q

記号	意味
$A$	与えられた実対称行列（ $A^{\mathsf T}=A$ ）
$Q$	正規直交行列： $Q^{\mathsf T}Q=I$ 、列ベクトルは互いに直交し、単位長さを持つ
$S$	対角行列： $S=\operatorname{diag}(\lambda_1,\dots,\lambda_n)$

書き方 $A=Q S Q^{\mathsf T}$ は 正規相似対角化 と呼ばれ、幾何学的には「座標系を回転（または鏡像）させる → A は独立した伸縮だけが残る」ということです。

1. なぜ「実対称行列は必ず正規対角化できる」のか？

スペクトル定理：

任意の実対称行列 $A$ に対して、正規直交行列 $Q$ が存在し、 $Q^{\mathsf T} A Q$ は対角行列であり、対角成分は $A$ の固有値です。

実固有値：対称性により固有値はすべて実数です。
正規直交固有ベクトル：もし $\lambda_i \ne \lambda_j$ であれば、対応する固有ベクトルは必ず直交します。
重根も正規基を取れる：同じ固有値が複数のベクトルに対応する場合、それらが張る部分空間内で Gram–Schmidt を行うことで直交基を得ることができます。

文字のステップを逐条解析

ステップ	説明
1. $A$ のすべての固有値と固有ベクトルを求める	$\det(A-\lambda I)=0$ を計算してすべての $\lambda_i$ を得る；各 $\lambda_i$ に対して $(A-\lambda_i I)v=0$ を解いて固有ベクトルを求める。
2. 固有値を一定の順序で対角線上に配置することで対角行列 $S$ を得る	例えば、昇順に $S=\operatorname{diag}(\lambda_1,\dots,\lambda_n)$ と配置します。順序は重要ではなく、後で列ベクトルの順序と一致していれば良いです。
3. 異なる固有値に対応する固有ベクトルは互いに直交します；重根の固有ベクトルは Gram-Schmidt によって直交化し、単位化します	- $\lambda_i\neq\lambda_j$ の場合、対応するベクトルは自然に直交しており、変更は不要です。

$\lambda$ が重複している場合（幾何的重複度 >1）、適当に線形独立なベクトルの組を取り、その部分空間内で Gram-Schmidt を行い、互いに直交し、各自の長さを 1 にします。 |
| 4. 固有値の対角線上の順序に従って改造された固有ベクトルを横に並べることで、正規直交行列 $Q$ を得る | 対角線の固有値の順序に従って改造された固有ベクトルを列として配置し、 $Q=[q_1\ \cdots\ q_n]$ とします。このとき $Q^{\mathsf T}Q=I$ となり、 $A = Q S Q^{\mathsf T}$ となります。 |

$2 \times 2$ の具体的な小例

設定

A=\begin{bmatrix} 4 & 1\\ 1 & 4 \end{bmatrix}

① 固有値を求める

\det(A-\lambda I)=(4-\lambda)^2-1=0 \Longrightarrow \lambda_1=5,\; \lambda_2=3

② 固有ベクトルを求める

$\lambda_1=5$ ： $(A-5I)v=0 \ \Rightarrow\ v_1=\begin{bmatrix}1\\1\end{bmatrix}$
$\lambda_2=3$ ： $(A-3I)v=0 \ \Rightarrow\ v_2=\begin{bmatrix}1\\-1\end{bmatrix}$

③ 単位化

q_1=\frac{1}{\sqrt2}\begin{bmatrix}1\\1\end{bmatrix},\quad q_2=\frac{1}{\sqrt2}\begin{bmatrix}1\\-1\end{bmatrix}

④ 組み立てて検証

Q=\frac1{\sqrt2}\begin{bmatrix} 1 & 1\\ 1 & -1 \end{bmatrix},\quad S=\begin{bmatrix}5&0\\0&3\end{bmatrix},\quad Q^{\mathsf T} A Q = S.

6. 行列式（det・）#

行列式（determinant）は、正方行列 $A$ をスカラー $\det A$ にマッピングする演算です。
このスカラーは行列の最も核心的な幾何学的および代数的情報を統合しています：体積の伸縮因子、可逆性、固有値の積など。

公式

階数	公式
$1\times1$	$\det[a]=a$
$2\times2$	$\displaystyle\det\!\begin{bmatrix}a&b\\c&d\end{bmatrix}=ad-bc$
$3\times3$	「サルス法」または第一行に沿って展開：
$\displaystyle \det\!\begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix}=a(ei-fh)-b(di-fg)+c(dh-eg)$
核心的性質（すべての定義が満たすべき条件）

性質	説明
乗法性	$\det(AB)=\det A\cdot\det B$
可逆判定	$\det A\neq0 \iff A$ は可逆
行列の線形性	各行（列）は要素に関して線形
交替性	2 行（列）を交換すると ⇒ 行列式の符号が変わる
対角線の積	上 / 下三角行列： $\det A=\prod_{i}a_{ii}$
固有値の積	$\det A=\lambda_1\lambda_2\cdots\lambda_n$ （重複を含む）

3×3 手計算の例

設定

A=\begin{bmatrix} 2 & 1 & 3\\ 0 & 4 & -1\\ 5 & 2 & 0 \end{bmatrix}

第一行に沿って展開します：

\begin{aligned} \det A &= 2\;\det\!\begin{bmatrix}4&-1\\2&0\end{bmatrix} \;-\;1\;\det\!\begin{bmatrix}0&-1\\5&0\end{bmatrix} \;+\;3\;\det\!\begin{bmatrix}0&4\\5&2\end{bmatrix} \\[4pt] &= 2\,(4\cdot0-(-1)\cdot2) -1\,(0\cdot0-(-1)\cdot5) +3\,(0\cdot2-4\cdot5) \\[4pt] &= 2\,(2) -1\,(5) +3\,(-20) \\[4pt] &= 4 - 5 - 60 = -61. \end{aligned}

一言でまとめる

「行列式を取る」とは： $n\times n$ の正方行列を一連の交替的かつ線形な規則に従って単一の数字に圧縮することです。この数字は行列の体積の伸縮、方向、可逆性、固有値の積などの重要な情報を同時にエンコードしています。

7. 行列のランク#

行列の「ランク」とは一体何でしょうか？

等価な視点	直感的な説明
線形独立	行（または列）の中からどれだけの互いに線形独立なベクトルを選べるかがランクです。
空間の次元	列ベクトルが張る部分空間（列空間）の次元 = 行ベクトルが張る部分空間（行空間）の次元 = ランク。
満ランクの行列式	行列内の最大の非零行列式の階数 = ランク。
特異値	SVD $A=U\Sigma V^{\!}$ において、非零特異値*の個数 = ランク。

線形独立
以下に 3 × 3 の小さな行列を用いて 3 つの対比例を示し、「ランク = どれだけの線形独立な列（または行）ベクトルを選べるか」ということを明確にします。

| 行列 $A$ | 列ベクトルを $\bigl(v_1\,|\,v_2\,|\,v_3\bigr)$ として書く | 線形関係 | ランク |
|------------|-----------------------------------------------|-----------|--------|
| $\displaystyle\begin{bmatrix}1&2&3\\2&4&6\\3&6&9\end{bmatrix}$ | $v_1=\begin{bmatrix}1\\2\\3\end{bmatrix}$
$v_2=\begin{bmatrix}2\\4\\6\end{bmatrix}=2v_1$
$v_3=\begin{bmatrix}3\\6\\9\end{bmatrix}=3v_1$ | 3 つの列はすべて同一直線上にあります ——独立なベクトルは 1 つだけ | 1 |
| $\displaystyle\begin{bmatrix}1&0&1\\0&1&1\\1&1&2\end{bmatrix}$ | $v_1=\begin{bmatrix}1\\0\\1\end{bmatrix}$
$v_2=\begin{bmatrix}0\\1\\1\end{bmatrix}$
$v_3=v_1+v_2$ | $v_1, v_2$ は共線ではない ⇒ 2 次元平面； $v_3$ はこの平面内にあります | 2 |
| $\displaystyle\begin{bmatrix}1&0&1\\0&1&1\\1&1&0\end{bmatrix}$ | $v_1=\begin{bmatrix}1\\0\\1\end{bmatrix}$
$v_2=\begin{bmatrix}0\\1\\1\end{bmatrix}$
$v_3=\begin{bmatrix}1\\1\\0\end{bmatrix}$ | 任意の 2 列は第三列を線形に表現できない ⇒ 3 つの列は全体で $\mathbb R^{3}$ を張ります | 3 |

「無関係」を判断する方法は？

手計算 列を行列にまとめ、消去を行います → 非零行の数がランクです。
概念もし定数 $c_1,c_2,c_3$ が存在して $c_1v_1+c_2v_2+c_3v_3=0$ かつ全てが 0 でない場合、ベクトルは関連しています；そうでなければ無関係です。
- ケース 1：$2v_1-v_2=0$ → 関連
- ケース 2：$v_3=v_1+v_2$ のみが関連し、$v_1,v_2$ は無関係
- ケース 3：どの非自明な組み合わせも ≠ 0 → 3 つのベクトルは全て独立

一言で言えば：ランク = この行列が実際に「保持できる」独立した情報の量（次元）。

8. 低ランク近似#

なぜ SVD を切り捨てる（低ランク近似）と、k (m+n)+k 個の数だけ保存すればよいのか？

元の行列

A\in\mathbb R^{m\times n}

をランク $k$ に切り捨てて次のように書きます

A_k \;=\; U_k \,\Sigma_k \, V_k^{\mathsf T},

ブロック	形状	保存する必要のあるスカラーの数	説明
$U_k$	$m\times k$	$m \times k$	左特異ベクトル：最初の $k$ 列のみを取ります
$V_k$	$n\times k$	$n \times k$	右特異ベクトル：同様
$\Sigma_k$	$k\times k$ 対角	$k$	対角線上の $k$ 個の特異値のみを保持します

これら 3 つを合計すると

\underbrace{m k}_{U_k} \;+\; \underbrace{n k}_{V_k} \;+\; \underbrace{k}_{\Sigma_k} \;=\; k\,(m+n)+k.

$U_k$ と $V_k$ ：それぞれ $k$ 列を持ち、各列は行数の長さのベクトルを保存します
$\Rightarrow mk + nk$ 個の数。
$\Sigma_k$ ：対角行列で、 $k$ 個の対角要素のみが必要です —— $k^2$ ではありません。

したがって、ランク - $k$ の SVD 近似を用いて元の $m\times n$ の保存量を置き換えると、パラメータ量は $mn$ から $k(m+n)+k$ に縮小されます。
$k \ll \min(m,n)$ の場合、節約されるスペースは非常に大きくなります。

ランクの低下 = 情報の次元の低下、低ランクの保存 = パラメータ量 / メモリの同時低下

9. ノルム#

「二重縦線」 $|,\cdot,|$ は線形代数において ノルム（norm） を表します。

ベクトル $v\in\mathbb R^m$ に対して、最も一般的なのは 二ノルム（Euclidean norm）： $\|v\|=\sqrt{v^{\mathsf T}v}=\sqrt{\sum_{i=1}^{m}v_i^{2}},\qquad \|v\|^{2}=v^{\mathsf T}v.$
図中の $\|Xw-y\|^{2}$ は、ベクトル $Xw-y$ の各成分を平方して合計することを意味します。
行列 $A$ に対して $\|A\|$ と書かれる場合、通常は フロベニウスノルムを意味します： $\|A\|_F=\sqrt{\sum_{i,j}A_{ij}^{2}}$ 。ただし、この図ではベクトルに関するものです。

対比すると、単一の縦線 $|\,\cdot\,|$ は通常、絶対値（スカラー）または行列式 $|A|$ を表します。したがって、二重縦線はベクトル / 行列の「長さ」の記号であり、単一の縦線はスカラーの大きさまたは行列式の記号です —— 対象と意味が異なります。

ベクトルの一般的なユークリッド距離 -- 2 ノルム（L2 ノルム）#

import torch

b = torch.tensor([3.0, 4.0])
print(b.norm())  # 出力 5.0

.norm() は PyTorch テンソル（torch.Tensor） のメソッドです。

行列の一般的なフロベニウスノルム#

行列にも「長さ」があります —— 一般的なのは フロベニウスノルム

名称	記号	公式（対 $A\in\mathbb R^{m\times n}$ ）	ベクトルとの類似
フロベニウスノルム	$\displaystyle\|A\|_F$	$\displaystyle\sqrt{\sum_{i=1}^{m}\sum_{j=1}^{n}A_{ij}^{2}}$	ベクトルの 2 ノルム $\|v\|=\sqrt {\sum v_i^2}$ のように

1. なぜ「行列の内積」としても書けるのか

行列空間で一般的に用いられる内積は

\langle A,B\rangle := \operatorname{tr}\!\bigl(A^{\mathsf T}B\bigr),

ここで $\operatorname{tr}(\cdot)$ はトレース演算（対角線要素の和）です。
$A$ 自身にこの内積を与えると、

\|A\|_F^{2} \;=\;\langle A,A\rangle \;=\;\operatorname{tr}\!\bigl(A^{\mathsf T}A\bigr).

したがって：

$\boxed{\;\|A\|_F^{2}= \operatorname{tr}(A^{\mathsf T}A)\;}$

これは行列版の $\|v\|^{2}=v^{\mathsf T}v$ であり —— ただし、ベクトルの内積を「トレース内積」に置き換えたものです。
フロベニウスノルムは実際にすべての特異値の平方和の平方根に等しい、すなわち：

\| A \|_F = \sqrt{\sum_i \sigma_i^2}

ここで：

$| A |_F$ は行列 $A$ のフロベニウスノルムです
$\sigma_i$ は $A$ の特異値です

フロベニウスノルムは実際にすべての特異値の平方和の平方根に等しい
展開して説明します：

フロベニウスノルムは次のように定義されます：

\| A \|_F = \sqrt{ \sum_{i,j} |a_{ij}|^2 }

しかし特異値分解（SVD）は次のように教えてくれます：

A = U \Sigma V^T

ここで $\Sigma$ は対角行列で、主対角線上には特異値 $\sigma_1, \sigma_2, \dots$ が並んでいます。

フロベニウスノルムは変換しない（単位正規直交変換はノルムを変えない）ため、次のように直接計算できます：

\| A \|_F^2 = \sum_{i,j} |a_{ij}|^2 = \sum_i \sigma_i^2

したがって最終的に：

\| A \|_F = \sqrt{ \sum_i \sigma_i^2 }

注意すべき落とし穴

注意：
✅ 単一の特異値の平方根ではなく、最大特異値でもありません
✅ すべての特異値を平方して合計した後に平方根を取ります

スペクトルノルムは「最も拡大する方向」を見ますが、フロベニウスはすべてのエネルギーを累積します。

行列のスペクトルノルム#

✅ スペクトルノルムの定義

行列 $A$ のスペクトルノルム（spectral norm）は次のように定義されます：

\| A \|_2 = \max_{\|x\|_2 = 1} \| A x \|_2

直訳すると、行列 $A$ が単位ベクトルをどれだけ長く引き伸ばすかの最大値です。
特異値はもともと行列の引き伸ばし変換を表しています。

これは $A$ の最大特異値に等しいです：

\| A \|_2 = \sigma_{\max}(A)

別の視点：スペクトルノルム ≈ 単位ベクトルを行列に入れたときに引き伸ばされる最大の長さ
✅ フロベニウスノルムとの関係

フロベニウスノルム → 全体のエネルギー（行列要素の平方和）を見ます。
スペクトルノルム → 単一の方向での最大の引き伸ばし量を見ます。

言い換えれば：

フロベニウスは行列の「体積」の総量を表します。
スペクトルノルムは「最も極端な」単一方向の拡大率を表します。

✅ 例：なぜ重要なのか？

神経ネットワークの線形層 $W$ を想像してください：

$\| W \|_2$ が非常に大きい場合、入力のわずかな摂動が拡大されます。
ネットワークは過剰適合しやすく、ノイズに敏感です。
$\| W \|_2$ が適度であれば、ネットワークの出力の変化は入力の摂動に対して安定し、
一般化能力が向上します。

したがって、現代の手法（例えばスペクトル正規化）は、
トレーニング中に $W$ のスペクトルノルムをある範囲に抑えることを直接行います。

⚠ 欠点を率直に述べる

スペクトルノルムは非常に強力ですが：

単一の最大方向にのみ注目し、他の方向の拡大を無視します；
フロベニウスノルムよりも計算が複雑です（特異値分解が必要で、単純な要素の平方和ではありません）。

概要の比較

	ユークリッドノルム (2-norm, ‖v‖)	フロベニウスノルム (‖A‖_F)
対象	ベクトル $v\in\mathbb R^{n}$	行列 $A\in\mathbb R^{m\times n}$
定義	$\displaystyle\\|v\\|=\sqrt{\sum_{i=1}^{n}v_i^{2}}$	$\displaystyle\\|A\\|_F=\sqrt{\sum_{i=1}^{m}\sum_{j=1}^{n}A_{ij}^{2}}$
等価な表現	$\\|v\\|^{2}=v^{\mathsf T}v$	$\\|A\\|_F^{2}=\operatorname{tr}(A^{\mathsf T}A)=\sum_{k}\sigma_k^{2}$
幾何学的意味	ベクトルの $n$ 次元ユークリッド空間における長さ	行列要素を「長いベクトル」として見るときの長さ
単位 / 尺度	座標軸と同じ尺度を持つ	同上；行列の形状に依存しない
一般的な用途	誤差測定、正則化 $L^2$ 、距離	重み減衰、行列近似誤差、カーネル法
スペクトルノルムとの関係	$\\|v\\|=\sigma_{\max }(v)$ (単一の特異値のみ)	$\\|A\\|_F\ge \\|A\\|_2=\sigma_{\max }(A)$ ；ランク = 1 の場合は等しい

1. 同じ考え方、異なる次元

ユークリッドノルムは ベクトル自身と自分自身の内積を取った後に平方根を取ります。
フロベニウスノルムは行列の各要素を長いベクトルとして見て、同じことを行います；行列言語で書くと

$\|A\|_F=\sqrt{\operatorname{tr}(A^{\mathsf T}A)}.$

これは「転置 → 乗算 → トレースを取る」ということです。

2. どのような場合にどちらを使用するか？

シーン	推奨ノルム	理由
予測誤差、勾配降下	ユークリッド (ベクトル残差)	残差は自然に列ベクトルです
ネットワークの重み正則化 (Dense / Conv)	フロベニウス	パラメータの形状に関心がなく、全体の大きさのみを気にします
行列近似の質を比較 (SVD, PCA)	フロベニウス	特異値の平方和に簡単に対応します
安定性 / リプシッツ境界	スペクトルノルム ( $\\|A\\|_2$ )	拡大率に関心があり、全体のエネルギーには関心がありません

3. 直感的な違い

ユークリッド：量 単一の方向 の長さ；
フロベニウス：量 各要素のエネルギー の総和であり、したがって行列にとっては、どの列や行も特別ではなく、すべての要素が同じように扱われます。

一言で記憶する：

ユークリッドノルム：ベクトルの「定規」。
フロベニウスノルム：行列を「平らにして」同じ定規でその全体の大きさを測る。

10. 行列の積の転置#

行列代数において、2 つ（または複数）の行列の積の転置には固定の「反転順序」ルールがあります：

(AB)^{\mathsf T}=B^{\mathsf T}\,A^{\mathsf T}.

つまり 各行列を転置した後、乗法の順序を逆にします。
この性質は、任意の次元に一致する実（または複素）行列に対して成り立ち、再帰的に拡張できます：

(ABC)^{\mathsf T}=C^{\mathsf T}\,B^{\mathsf T}\,A^{\mathsf T},\qquad (\,A_1A_2\cdots A_k)^{\mathsf T}=A_k^{\mathsf T}\cdots A_2^{\mathsf T}A_1^{\mathsf T}.

xLog 編集 Markdown 文書の注意点

すべての数学表現が $$ … $$ を使用していることを確認してください。
$n \times n$ のような単一の $ がある場合は、n × n または $$n\\times n$$ に変更します。

参考動画：

こちらをクリックして B 站の動画を見る